머신러닝 (Based on: Coursera - Andrew Ng)
-
 : 코세라에서 강의(강사: Andrew Ng)하는 머신러닝에 대한 이해를 요약함.
: 코세라에서 강의(강사: Andrew Ng)하는 머신러닝에 대한 이해를 요약함.
01. 지도 학습(Supervised Learning)과 비지도 학습(Unsupervised Learning)
01-1. 지도 학습(Supervised Learning)
지도 학습(Supervised Learining) 은 크게 회귀(Regression)와 분류(Classification)로 나뉜다. 회귀와 분류의 차이는 종속변수(반응변수)가 연속형(Continuous)인가 이산형(Discrete)인가에 따라 다르다고 할 수 있다. 우선 둘 다 현재의 자료를 바탕으로 미래를 예측한다는 것은 동일하다.
회귀는 종속변수가 연속형일 경우이고, 분류는 종속변수가 이산형일 때라고 볼 수 있다. 그랬을 때 로지스틱 회귀분석이 회귀분석이 회귀분석모형을 사용하지만, 분류인가에 대한 의문이 들 수 있다. 결론부터 말하자면, 분류에 사용되는 방법이다.
이 부분은 분류(Classification)-로지스틱 회귀분석(Logistic Regresstion) 부분에서 알 수 있다.
- 종속변수가 이산형: 분류(Classification)
- 종속변수가 연속형: 회귀(Regression)
01-2. 비지도 학습(Unsupervised Learning)
비지도 학습(Unsupervised Learning) 은 문제에 대한 해결 방법을 거의 또는 전혀 알지 못할 때, 결과가 어떠할 것인지를 예측하는 것이다. 우리는 설명변수가 어떤 영향을 미칠 지 모르는 상황(즉, 종속변수가 없는 상황) 속에서 해당 자료(Data)의 구조를 찾기 위해 비지도 학습을 사용한다.
비지도 학습은 크게 군집(Clustering)과 비군집(Non-Clustering)으로 나뉜다. 군집은 자료 내 변수들(Variables) 간의 관계(Relationship)를 파악하여 군집을 구성하는 것이고, 비군집은 ‘칵테일 파티 효과(Cocktail Party Effect)’를 예로 들 수 있다. 여러 노이즈로 생각되는 값들 중에서 특정값을 찾아내고 이를 강조(Amplify)하는 것으로 실제 신경과학(Neuroscience)에서 관심을 갖고 있는 부분이고, 이를 구현하는 ‘칵테일 파티 알고리즘’(Cocktail Party Algorithm)이 있다.
02. 모델 구현(Model Representation)
향후 개념 설명을 위해, 다음과 같이 변수를 설명한다.
- $\boldsymbol{x^{(i)}}$는 입력값(Input, 설명변수)을 나타내며, 우리가 입력하는 변수임.
- $\boldsymbol{y^{(i)}}$는 출력값(Output, 반응변수)을 나타내며, 우리가 예측하고자 하는 값임.
- $\boldsymbol{(x^{(i)}, y^{(i)})}$는 훈련 예제(Training Example)이며, 우리가 학습을 시킬 데이터 세트(Dataset)임.
- $m$ 개의 훈련 예제 목록인 $\boldsymbol{(x^{(i)}, y^{(i)});\; i=1,…,m}$은 훈련 세트(Training Set)라고 함.
- 윗첨자(Superscript) $\boldsymbol{^{(i)}}$는 훈련 세트의 인덱스(Index)를 나타내며, 승수(Exponentiation, 누승법/멱법)와는 관계가 없음.
- $\boldsymbol{X}$는 입력값들의 공간(Space, 집합(Set)으로 생각해도 무방할 듯함.)을 나타내며, $\boldsymbol{Y}$는 출력값들의 공간을 나타냄.
- 여기서 $X$와 $Y$는 실수 공간임(정확히는 실수 공간에 존재함.).
- 즉, $\boldsymbol{X=Y=\mathbb{R}}$이라고 하나, $\boldsymbol{X\subset Y\subset \mathbb{R}}$이 더 정확할 것 같은데 지극히 ‘사견’임.
- 우리의 목표는 주어진 훈련 세트로 $\boldsymbol{h: X \rightarrow Y}$ 함수를 잘 학습하는 것이며, $\boldsymbol{h(x)}$는 $y$에 대응하는 값에 대한 좋은("good") 예측기(Predictor)임.
- 역사로 $\boldsymbol{h}$는 가정(Hypothesis, '예측'으로 변환함.)을 뜻함.

03. 비용 함수(Cost Function)
비용 함수(Cost Function)을 활용하여, 예측 함수($h_{\theta}(x^{(i)})$)의 정확도를 측정한다. 비용 함수는 ‘$x$를 입력값으로 한 예측의 결괏값’과 ‘실젯값 $y$’의 차이의 평균(산술평균과는 다름.)으로 나타낸다.
$J(\theta_{0},\theta_{1}) = \frac{1}{2m}\sum_{i=1}^{m}(\hat{y}^{(i)}-y^{(i)})^{2} = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2}$
이 함수는 ‘제곱 오차 함수(Squared Error Funciton)’, 또는 ‘평균 제곱 오차(Mean Squared Error)’라고도 불린다. 이 평균값은 이후 해당 값을 미분하여 계산하는 경사 하강법(Gradient Descent)의 계산을 쉽게 하기 위해 $\frac{1}{2}$로 나눠준다.(미분을 하면 제곱에서 떨어지는 2와 상쇄됨)
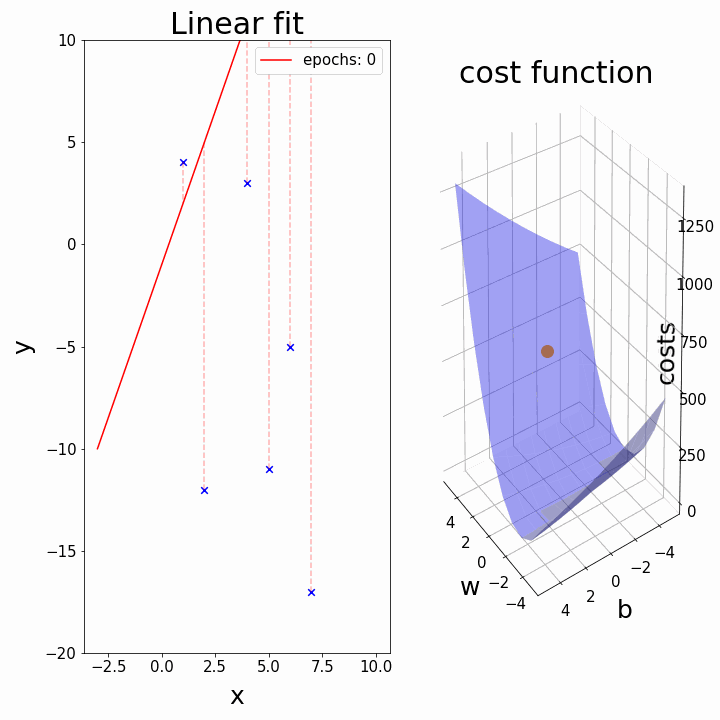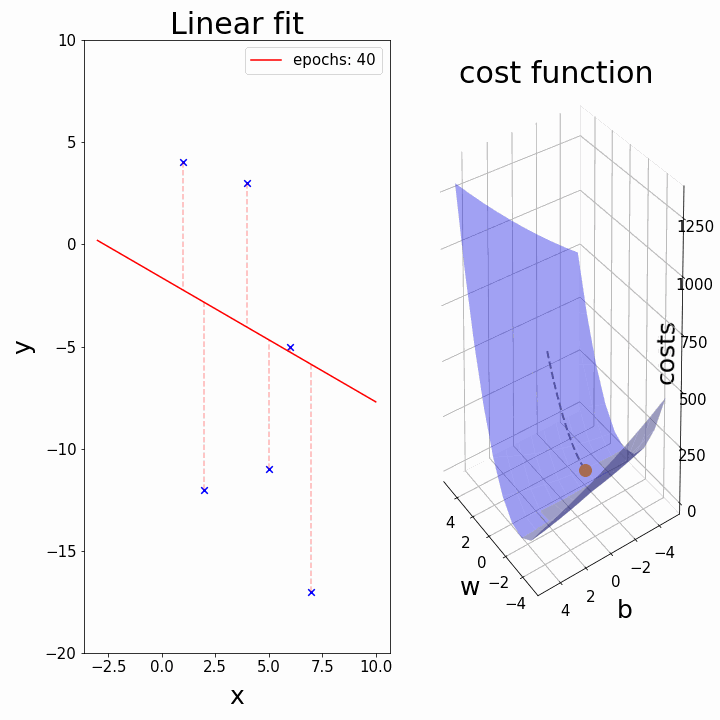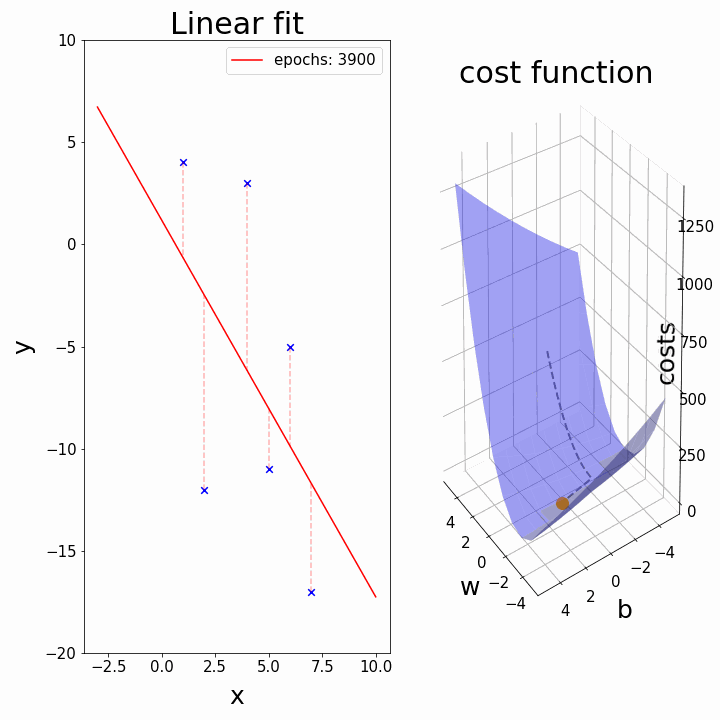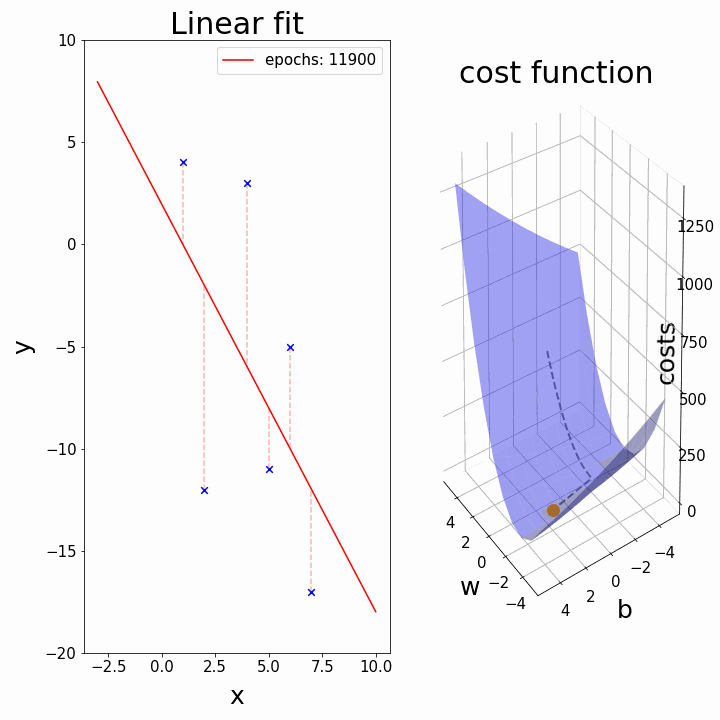
비용 함수에 대한 내용을 다음에서 시각화하여, 조금 더 자세히 알아보자.
예시03-1. (비용 함수 시각화 설명: 절편($\theta_{0}$) 미고려)
|훈련 데이터 세트는 $x$-$y$ 평면에 산포되어(흩어져) 있다. 우리는 $h_{\theta}(x)$로 표현되는 산포된 데이터 점들을 잘 설명하며 통과하는 직선(추세를 나타내는 직선)을 그리고자 하는 것이다. 이러한 최적의 직선은 산포된 점들로부터의 (가로축을 기준으로)수직방향으로의 거리가 최소가 되는 것이다. 아래와 같이 $(x, y)$를 나타내는 점이 세 개($(1, 1), (2, 2), (3, 3)$)가 있다고 가정하자. 이러한 분포를 가장 잘 설명하는 직선은 아래 그림과 같을 것이다.|
| 1. $\theta_{1}$이 1일때 추정선은 모든 점들을 다 지나간다. |

| 2. 1에 대한 비용함수 값은 0이 된다. |

| 3. $\theta_{1}$이 0.5일때 추정선은 실제값과 아래와 같이 차이를 낸다. |

| 4. 3에 대한 비용함수 값은 그 차이의 제곱합에 $\frac{1}{2}$을 곱한 만큼 차이가 난다. |

| 5. 이렇게 계속해서 $\theta_{1}$을 바꿔주며 추정값과 실제값의 차이(비용함수)를 구하면, $\theta_{1}$과 비용함수($J(\theta_{1})$)의 관계는 아래 그림과 같이 나타낼 수 있다. |

예시03-2. (비용 함수 시각화 설명: 절편($\theta_{0}$)까지 고려)
|준비중|
04. 파라미터 학습(Parameter Learning)
04-1. 경사 하강법(Gradient Descent)
실젯값을 잘 추정하는 선을 그리기 위해선 적절한 파라미터의 조정이 필요하다. 실젯값과 추정값을 보여주는 식(2차원 평면을 가정했을 때)은 ‘$x$의 기울기’와 ‘$x$의 절편’으로 조정이 가능하다.(곡선의 경우에는 다항회귀로 $x$의 차원을 높여주는 것이므로 여기서는 논외로 한다.) 즉, 앞서 배웠던 비용 함수에서, $\theta$ 값들을 조정하여 $J(\theta)$값이 최소가 되는 $\theta$들을 찾아 실젯값을 추정하는 함수에 적용하면 되는 것이다.
정리하자면, 결국 아래 그림과 같이 비용함수를 최소로 하는 $\theta$들을 찾으면 된다는 말이다. 아래 그림은 랜덤하게 고른 $\theta$들의 값에서 최적의 비용함수를 갖는 $\theta$의 값으로 찾아가는 과정을 ‘+’표시로 추적한 것이다.

하지만 위 그림과 같이 $\theta_{1}$이 $1$에 가까운 쪽에 있는 화살표가 실제로 찾아간 곳(‘+’ 표시가 있는 곳)의 화살표 보다 더 낮은 $J$값을 갖는다. 즉, 전자의 화살표가 가리키는 것이 전역 최솟값(Global Minimum)이라고 가정하면, 후자의 화살표가 가리키는 것은 지역(국부) 최솟값(Local Minimum)이다.
우리의 목표는 ‘전역 최솟값’을 찾는 것이다. 이를 위해 $\alpha$(learning rate)를 조정하여,
Leave a comment